
Transformations

Transformations
Using the graphing calculator to examine transformations:
|
||
|
1. Clear
entries in the Y= positions (or turn them
off).
2. Turn on the Connected Graph icon under StatPlots. |
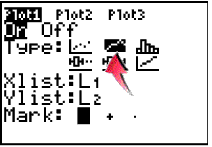 |
|
|
3. Enter values into L1 and L2. Enter the x-coordinate in L1 and its corresponding y-coordinate in L2. Enter the first coordinate again at the end to complete the connected drawing. (See Basic Commands for help entering data in lists.) The original triangle is now residing in Plot1. When graphing do NOT choose ZoomStat for the window. We want to have a coordinate axes for examining our transformations. Use a standard 10x10 window (ZStandard) for this problem. 4. We will be placing our transformation coordinates into L3 and our transformation figure will reside in Plot2. |
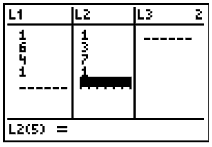 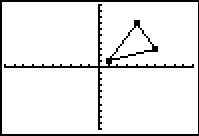 |
|
|
|
||
Store the negated y-values into list L3. You can type them in yourself or let the calculator create the values. Arrow up ONTO L3 and enter - L2 (to negate the y-values). Press ENTER.
Set up Plot2: Xlist: L1 and
Ylist: L3
|
||
Let L3 be -L1. Under Plot 2, assign Xlist: L3 and Ylist: L2. Graph.
|
||
Under Plot 2, assign Xlist: L2 and Ylist: Y1. Graph. Your might also wish to graph Y1= x to show the line of reflection. |
||
Let L3 = -L1. Let L4 = -L2. Under Plot 2, assign Xlist: L3 and Ylist: Y4. Graph. |
||
Let L3 = L1 - 7. Let L4 = L2 - 2. Under Plot 2, assign Xlist: L3 and Ylist: Y4. Graph. |
||
Let L3 = L1 * 2. Let L4 = L2 * 2. Under Plot 2, assign Xlist: L3 and Ylist: Y4. Graph. Adjust the window to see the dilation. |
||
![]()
Finding Your Way Around
TABLE of CONTENTS