|
Residuals and Least Squares
Developing a Model by Observation:
A simple type of regression equation is a straight line. A
scatter plot of the data is drawn, two points are chosen that "appear"
to lie on the line of best fit, the slope is determined and an
equation is written. This is known as a freehand method of
curve fitting. Unfortunately, different observers, who choose
different points, may obtain
different equations.
Developing a Model by Least
Squares:
To avoid individual judgment in curve fitting, it is necessary
to agree on a definition of a “best-fitting line” or curve. Consider
the following set of points:
|
|
For a given value of x, say x1, there will be a
difference between the value y1 and the corresponding value as
determined by the “best fitting” curve. This distance, D1, is
referred to as a residual.
A residual is the difference from the actual y-value
and the value obtained by plugging the x-value (that goes
with the y-value) into the regression equation.
Using these residuals, the
following definition has been developed:
Definition:
Of all curves approximating a given set of data
points, the curve having the property that
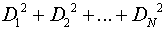
is a minimum is called a best-fitting curve.
|
A curve having
this property is said to fit the data in the least-squares sense and
is called a least-squares curve.
The graphing calculator uses this least squares process to determine
regression models. When regression models are computed,
residuals are automatically stored in a list called
RESID.
Note: For a perfect fit, the residuals will be all zero
and ZOOM 9: ZoomStat will result in a
WINDOW RANGE error since
Ymin = 0 and Ymax = 0. If you still wish to see the plot, change
Ymin = -1 and Ymax = 1 and then press GRAPH. |


![]()