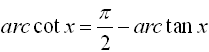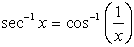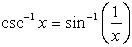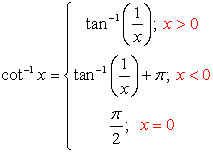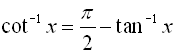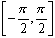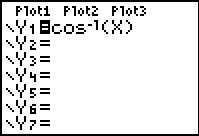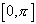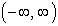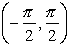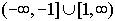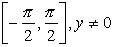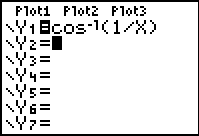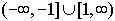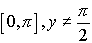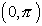|

Inverse Trig Functions
(also see Composition of
Inverse Trig Functions)
Inverse trig functions are also referred to as
arcfunctions. The notation may be:
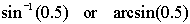
where each is interpreted as "the angle whose sine is 0.5".
| Find sin-1(0.5) in
degrees |
Set the MODE to Degree. Type on the Home Screen
 
The angle whose sine is 0.5 is 30º. But it could also be 150º,
390º, 510º, ...
If the problem was stated as Arcsin(0.5), where the A was
capitalized,
it would have been asking for the function Arcsin in
the interval [-90º, 90º] instead of the multi-valued relation arcsin.
When the notation is sin-1(0.5), you will need to read the
context of the problem.
| Find sec-1(3/2) in
degrees |
Be careful when working with the
inverses of the reciprocal trig functions. Their computations may
not be what you expect them to be. Observe:
| Arc Notation |
Exponent notation |
S O L U T I O N: Find sec-1(3/2) in
degrees.
Set the MODE to Degree. Type on the Home Screen
 
| Graph the inverse trig functions |
The graphing calculator is programmed to graph arcsin(x),
arccos(x) and arctan(x) as functions
(thus the domains are limited to ensure that the graphs pass the
vertical line test for functions).
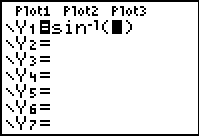
|
|
f (x)
= sin-1(x)
f (x)
= arcsin(x) |
|
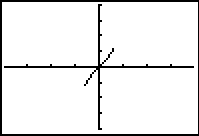 |
Domain: [-1,1]
Range: 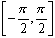 |
|
|
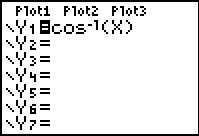
|
| f (x) = cos-1(x) f (x) = arccos(x) |
|
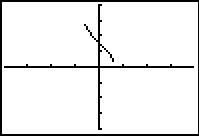 |
Domain: [-1,1]
Range: 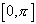 |
|
|
|
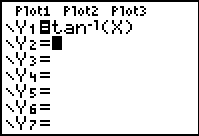
| f (x) = tan-1(x) f (x) = arctan(x) |
|
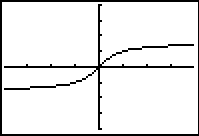 |
Domain: 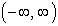
Range: 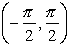 |
|
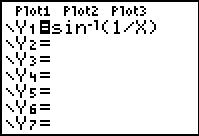 |
|
f (x)
= csc-1(x)
f (x)
= arccsc(x) |
|
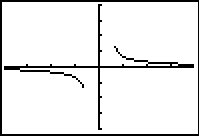 |
Domain: 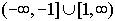
Range: 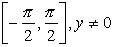 |
|
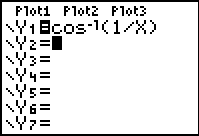 |
|
f (x)
= sec-1(x)
f (x)
= arcsec(x) |
|
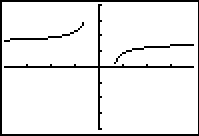 |
Domain: 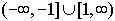
Range: 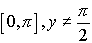 |
|
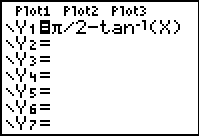 |
|
f (x)
= cot-1(x)
f (x)
= arccot(x) |
|
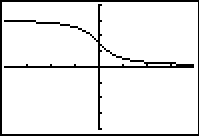 |
Domain: 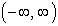
Range: 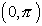 |
|
|

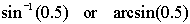


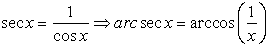
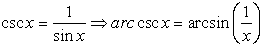
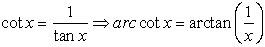 ,
,